کاربرد سری فرویه
توسعه نظریه سریهای مثلثاتی در 1822 ،با چاپ کتابی توسط فوریه آغاز شد.تحقیقات چندین ساله وی به گسترش نظریه وسیعی در مورد سریها منجر شدکه امروزه به نام خود وی معروف ،و از اهمیت بسیاری در ریاضیات ،علوم و فن برخوردار است.ایده اساسی این نظریه،معرفی توابع تناوبی یا دوره ای توسط توابع تناوبی(مثلثاتی) خاص است.
سری فوریه برای بررسی حرکات تناوبی در آکوستیک یا صوت شناسی،الکترودینامیک ،اپتیک یا نور شناسی، ترمودینامیک و غیره مورد استفاده قرار گرفته است.
در مهندسی الکتریک مسائلی چون رفتار بسامدی ،عناصر سوئیچینگ ،یا انتقال ضربه ها را میتوان به کمک سری فوریه حل کرد.
پیش بینی جزرومد در دریانوردی دارای اهمیت فراوانی است.از آنجا که اینها پدیده هایی تناوبی هستند از سری فوریه استفاده میشود و در تمام بندرهای مهم،وسائل مکانیکی چون پیش بینی کننده های جزر و مد ساخته میشود.امروزه کمتر شاخهای از فیزیک،ریاضیات، یا صنعت و فن وجود دارد که در آن از سریهای فوریه استفاده نشود.
تعریف
سری توابع 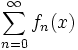 که جمله عمومی آن
که جمله عمومی آن
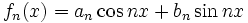
با ضرایب ثابت  و
و  است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول
است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول  همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی
همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی  ی را نشان میدهد.
ی را نشان میدهد.
این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد.
از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن،  ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب
،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب  و
و  و تابع مجموع
و تابع مجموع  به دست آورد.ضرب سری
به دست آورد.ضرب سری 
در عاملهای کراندار 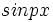 یا
یا 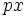 که در آنها p عددی صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان
که در آنها p عددی صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان 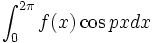 و
و 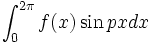
را با استفاده از انتگرالگیری جمله به جمله سری 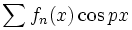 یا
یا 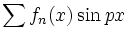 محاسبه کرد
محاسبه کرد
این انتگرالگیری ها شامل انتگرال های روی بازه 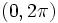 توابع
توابع 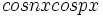 و
و 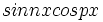 و
و 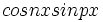 و
و 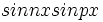 اند.
اند.





 )، آنگاه از سری فوریه به راحتی، عبارت زیر به دست میآید:
)، آنگاه از سری فوریه به راحتی، عبارت زیر به دست میآید:





 برگ درختان سبز در نظر هوشیار هر ورقش دفتری است معرفت کردگار
برگ درختان سبز در نظر هوشیار هر ورقش دفتری است معرفت کردگار