پسری که راه کوتاه را انتخاب کرد
پسر ها فریاد می کردند و همانطور که می دویدند در اطراف زمین بازی مدرسه می خندیدند. نزدیک آخر ترم مدرسه در آلمان بود در حدود دویست سال پیش .
بزودی مدرسه برای چند هفته تعطیل می شد و تعجبی ندارد که آنها(پسرها) احساس خوشحالی می کردند.
معلمشان از پنجره کلاس آنها را تماشا می کرد. او ابدا احساس خوشحالی نمی کرد. پایان ترم برای او، این معنی را می داد که مقدار زیادی کار باید انجام بدهد. او چه چیزی می توانست برای پسرها پیدا کند که انجام بدهند تا آنها را برای مدت طولانی ای ساکت و آرام نگه دارد؟ تا او بتواند به کارش برسد، ناگهان فکری به خاطرش رسید. وقتی که زنگ خورد برای پایان بازی ، اوداشت لبخند می زد و خوشحال بود.
یکی یکی پسرها به کلاس برگشتند و سر نیمکت ها نشستند. معلم گفت: گوش بدهید پسرها! من از شما می خواهم که مدادهایتان را بدست بگیرید و عددها را از یک تا صد بنویسید و بعد ازاینکه این کار را انجام دادید تمام آنها را جمع ببندید و صحبت نکنید و فکر کنید.
بمحض اینکه بچه ها کارشان را شروع کردند معلم لبخندی زد و گفت این باید آنها را برای مدتی مشغول کند. اما او در اشتباه بود!
پنج دقیقه بعد کند ترین (تنبل ترین) شاگرد هنوز داشت تاریخ را می نوشت و بیشتر بچه های دیگر تازه شروع کرده بودند به جمع کردن اعداد.
با وجود این یک پسر مدادش را پایین گذاشت.
معلم از او پرسید: "کاری" kari چی شده؟ نمی توانی بنویسی؟
پسر جواب داد نه آقا من تمام کرده ام! و جوابش می شود 5050 .
هیچ کس در کلاس حرف او را باور نمی کرد. چگونه می توانست یک پسر از بین ده تا این همه عدد را در این چنین مدت کوتاهی جمع کند؟
معلم به او گفت شاید بهتر باشد به ما بگویی که چگونه این عدد را بدست آورده ای؟
پسر گفت آسان بود!! قبل از همه چیر من عدد 1 و 99 را جمع بستم و شد 100 بعد من 2و 98 را جمع بستم و باز هم 100 آمد . د.باره من 3و 97 ،4و 96 را و همینطور ادامه دادم تا به 49و 51 رسیدم و هر دفعه من جواب صد را بدست می آوردم و به این ترتیب من چهل و نه تا 100 تا را بدست آوردم که می شود 4900. بعدا من دو شماره ای را که جا مانده بود جمع کردم یعنی 100و50 را و جواب 5050 را بدست آوردم. معلم نالید (فریاد کرد) و گفت بنظر می رسد که حق باپسر بود. حالا مجبور بود چیز دیگری برای آنها پیدا کند که انجام بدهند.
امروز ما اسم این معلم را فراموش کرده ایم. اما اسم پسر را که آنقدر در حساب سریع بود فراموش نکرده ایم. او اسمش –کاری گاوس – بود. ((kari gauss

کاری گاوس دانشمند مشهوری شد. یکی از بزرگترین علاقمندیش علم نجوم بود(مطالعه ستارگان) قبل از مرگش در سال 1855، او 155 کتاب نوشته بود.

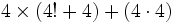


 برگ درختان سبز در نظر هوشیار هر ورقش دفتری است معرفت کردگار
برگ درختان سبز در نظر هوشیار هر ورقش دفتری است معرفت کردگار