مفهوم
تابع، در سراسر ریاضیات جدید و سایر علوم و در همه سطوح از اهمیت بسزایی برخوردار است. این مفهوم در ابتدا در
حساب دیفرانسیل و انتگرال که عمدتاً به مطالعه
توابع حقیقی و بررسی
حد و
مشتق و
انتگرال آنها میپردازد شکوفا شد.
آنچه ممکن است واژه تابع در ابتدا در ذهن خوانده کم و بیش آشنا با این مفهوم ایجاد کند، عبارتی چون f(x)=x2+sinx و سایر عبارات جبری است(البته به شرط تابع بودن) که عمدتاً بر اعداد حقیقی و یا مختلط تعریف شدهاند. اما این مفهوم بسیار گسترده تر از این است و این تنها بخش کوچکی از مفهوم تابع است.
در ابتدا مفهوم تابع چندان کلی نبود و اما در ادامه تلاشها برای ارائه تعریف و مفهومی کلی از تابع و گسترش نظریه مجموعهها، مفهومی ساده و کلی از تابع ارائه شد. این کلیت به قدری است که مثلاً برای مطالعه حساب دیفرانسیل و انتگرال باید شرایطی اضافی را بر تابع(مانند پیوستگی و مشتق پذیری) اعمال کرد تا رده خاصی از توابع مورد نظر برای مطالعه حاصل شود.
در بیشتر زمینههای ریاضی، اصطلاحات تبدیل و نگاشت نیز معمولاً با تابع هم معنی پنداشته میشوند. در هر حال ممکن است که در بعضی زمینههای خصوصیات دیگری داشته باشند. برای مثال در هندسه، یک نگاشت گاهی اوقات یک تابع پیوسته تعریف میشود.
معرفی مفهوم و بحث غیر رسمی
دو عبارت (y2=x (1 و (2) y=x2 را در نظر بگیرید که در آن x متغیری از اعداد حقیقی است.
در عبارت (1) اگر متغیر x را در عبارت قرار دهیم دو مقدار برای y حاصل میشود که عبارت اند از  ، اما در عبارت دوم با قرار دادن مقدار x مقداری یگانه برای y یعنی x2 حاصل میشود. به عنوان مثال در عبارت (1) اگر x=2 آنگاه
، اما در عبارت دوم با قرار دادن مقدار x مقداری یگانه برای y یعنی x2 حاصل میشود. به عنوان مثال در عبارت (1) اگر x=2 آنگاه  اما اگر در عبارت (2) قرار دهیم x=2 تنها یک جواب y=4 را بدست میآوریم.
اما اگر در عبارت (2) قرار دهیم x=2 تنها یک جواب y=4 را بدست میآوریم.
اگر متغییر x را ورودی و y مقدار حاصل از قرار دادن متغیر x را در عبارت، خروجی بنامیم و هر یک از عبارات را به عنوان قاعدهای بگیریم که هر ورودی x را طبق قانونی مشخص به خروجی y تبدیل میکند، میتوان تفاوت بین دو عبارت را به این صورت بیان کرد که در عبارت (1) برای هر ورودی x، قاعده مربوطه دو خروجی y را ارائه میدهد، در صورتی که در (2) برای هر ورودی x قاعده مربوط به آن دقیقاً یک خروجی y حاصل میشود.
در هر مورد قاعده را میتوان یک روش مشخص برای تناظر هر ورودی x به خروجی خودش در نظر گرفت.
رده خاصی از قواعد تناظر وجود دارند که به هر وروی خود یک و فقط یک خروجی نسبت میدهند. این نوع از قاعدهها از اهمیت خاصی برخوردارند چرا که برای هر ورودی، خروجی آنها یکتا و صریحاً قابل محاسبه و بیان است. چنین قواعدی را در اصطلاح تابع میگوییم.
پس بنابر آنچه تا کنون بیان شد یک تابع قاعدهای است که هر متغیر دریافتی خود را فقط به یک خروجی نسبت میدهد.

شکل(1) نمونهای از یک تناظر که تابع نیست
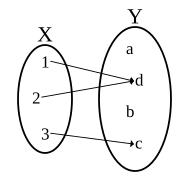
شکل(2) نمونهای از یک تابع
به عنوان مثال تناظر شکل(1) نمایش دهنده یک تابع نمیباشد چراکه عضو 3 به دو عضو متناظر شده است. اما شکل(2) نشان دهنده یک تابع است هر چند که دو عضو متفاوت به یک عضو نسبت داده شدهاند.
حال سعی میکنیم تعریفی دقیق و قابل قبول از نظر ریاضی برای این مفهوم پیدا کنیم. در این راه ابتدا نمادگذاری خاصی را معرفی میکنیم.
برای نمایش بهتر، تابع که خود یک قاعده برای تناظر است را با f نشان میدهیم و ورودی یا شناسه این تابع (قاعده) را با x نشان میدهیم که ممکن است عدد هم نباشد. یگانه مقدار خروجی که قاعده f به ورودی x نسبت میدهد را بجای y اینبار با (f(x نشان میدهیم و آن را مقدار تابع f در x یا تصویر x تحت تابع f میگوییم. همچنین از این پس به قاعدهای که هر x را به (y=f(x نسبت میدهد ضابطه تابع میگوییم.
برای مثال عبارت f(x) = x۲ نشان دهنده ضابطه یک تابع است، که در آن f شناسه x را دریافت میکند و آن را به x۲ نسبت میدهد. در این صورت برای ورودی ۳ مقدار f(3)=9 به دست میآید.
نکته قابل توجه این است که نباید تابع را با ضابطه آن اشتباه کرد. به عنوان مثال در مثال فوق f معرف خود تابع و عبارت (f(x معرف ضابطه تابع است.
همانطور که در ابتدا بیان شد، در یک تابع لزومی ندارد که حتماً بر روی اعداد علمیاتی انجام گیرد. به عنوان مثال تناظری که بین هر فرد و شماره شناسنامه آن وجود دارد نیز نمونهای از توابع است. در ادامه نمونه های بیشتری را از این نوع توابع در ریاضیات خواهید دید.
تا کنون مفهومی جالب توجه به نام تابع پیدا کردیم و به توصیف اجمالی آن پرداختیم. حال با در دست داشتن این مفهوم باید سعی در تعریف دقیق و قابل قبول آن از نظر ریاضی بکنیم.
تابع را به عنوان یک قاعده تناظر تعریف کردیم که به هر عضو ورودی خود یک عضو یگانه را متناظر میکند. حال میتوان همه عناصری را که به عنوان ورودی تابع قرار میگیرند در یک مجموعه قرار داد. در اختیار داشتن چنین مجموعهای مفید است و باعث میشود متغیرهایی که به عنوان ورودی تابع در نظر گرفته میشوند را تعیین کنیم و عناصر اضافه را حذف کنیم. چنین مجموعهای را دامنه تابع میگوییم. دامنه تابع f را با domf نشان میدهیم. به همین صورت میتوان مجموعه همه خروجیهای تابع که تصویر عناصر دامنه هستند را هم در نظر گرفت که به آن برد تابع گفته میشود و آن را با ranf یا Imf نشان میدهیم. (در خصوص این مفاهیم در ادامه دقیقتر بحث خواهد شد.)
حال تابع را میتوان به عنوان قاعدهای خاص برای تناظر بین اعضای دو مجموعه دامنه و برد تعریف کرد. به بیان دقیق تر، اگر A و B دو مجموعه باشند، یک تابع از مجموعه A به مجموعه B را میتوان قاعدهای تعریف کرد که به هر عضو مجموعه A چون a یک و فقط یک عضو از مجموعه B را چون (f(a نسبت میدهد. تابع f از مجموعه A به مجموعه B را با  نشان میدهیم.
نشان میدهیم.
اگر f تابعی از مجموعه A به مجموعه B باشد، A را دامنه f میگوییم. اما مجموعه B میتواند مجموعه ای بیش از برد تابع باشد. f به هر عضو A یک عضو یکتا از B را نسبت میدهد اما تضمینی وجود ندارد که هر عضو مجموعه B الزاماً تصویر یک عضو از A تحت f باشد. پس در حالت کلی برد تابع f زیرمجموعهای از مجموعه B است. مجموعه B را که برد تابع زیرمجموعهای از آن است را همدامنه تابع f میگوییم و آن را با codomf نشان میدهیم. طبق آنچه بیان شد، برد تابع زیرمجموعهای از همدانهاش است. میتوان دید که برد یک تابع یکتا است ولی همدامنه آن چنین نیست.
به عنوان مثال تابع  را با ضابطه f(x)=x2 در نظر بگیرید. دامنه این تابع مجموعه اعداد حقیقی است اما آیا برد آن نیز همان مجموعه اعداد حقیقی R است؟ پاسخ آشکارا منفی است چون اعداد حقیقی منفی، چون 1- تصویر هیچ عدد حقیقی تحت f نمیباشند. برد این تابع مجموعه اعداد حقیقی نامنفی است که زیرمجموعهای از اعداد حقیقی است.
را با ضابطه f(x)=x2 در نظر بگیرید. دامنه این تابع مجموعه اعداد حقیقی است اما آیا برد آن نیز همان مجموعه اعداد حقیقی R است؟ پاسخ آشکارا منفی است چون اعداد حقیقی منفی، چون 1- تصویر هیچ عدد حقیقی تحت f نمیباشند. برد این تابع مجموعه اعداد حقیقی نامنفی است که زیرمجموعهای از اعداد حقیقی است.
به نظر میرسد بیشتر قسمتهای تعریف اولیهای که از تابع ارائه دادیم را دقیق نمودیم و آنها را بر پایه مجموعه ها تعریف کردیم. اما نکتهای که هنوز در تعریف فعلی ما از یک تابع از مجموعه A به مجموعه B، به عنوان: «قاعدهای که به هر عضو مجموعه A یک و فقط یک عضو از مجموعه B را تناظر دهد.»
آزار دهنده و نادقیق است عباراتی چون «قاعده» یا «تناظر» است که از نظر ریاضی نادقیق هستند. چگونه میتوان این قاعده و بعد از آن تناظری که این قاعده معرف آن است را به طور دقیق فرمول بندی کرد.
فرض کنید f:A→B یک تابع باشد. در این صورت تابع f با انتخاب یک عضو a∈A آن را طبق ضابطه خود به عضو یکتای f(a)∈B متناظر میکند. میتوان هر عضو a را بوسیله زوج مرتب ((a,f(a) به (f(a نسبت دهیم. به این ترتیب، ممکن است معنی دقیق تناظر را ندانیم ولی به نظر طبیعی میرسد که تناظری که تابع f بین اعضای A و B ایجاد میکند را بوسیله زوج های مرتب ((a,f(a) برای هر a∈A تعریف کنیم.
حال تابع f به عنوان قاعده این تناظر، چیزی بجر توصیف نحوه تناظر اعضای A به B نیست که به طور کامل بوسیله همه زوجهای مرتب ((a,f(a) برای هر a∈A مشخص میشود پس تابع f را میتوان به عنوان مجموعه همه این زوجهای مرتب، یعنی مجموعه همه زوجهای مرتبی که مولفه اول آنها عضو A بوده و مولفه دوم آنها تصویر مولفه اول تحت تابع f است، تعریف کرد. شرط تابع بودن تضمین میکند که هیچ دو زوج متمایزی در تابع f دارای مولفه اول یکسان نخواهند بود.
همچنین از اینجا بنا به تعریف حاصل ضرب کارتی دو مجموعه A و B چون a∈A و f(a)∈B میتوان نوشت a,f(a))∈A×B). پس تابع f را میتوان به عنوان زیرمجموعهای از ضرب دکارتی دو مجموعه A و B در نظر گرفت. به عبارت دقیق تر تابع f را میتوان به عنوان رابطهای دو تایی از A به مجموعه B در نظر گرفت.
در این صورت در تابع f:A→B برای هر a∈A عبارت a,b)∈f) را به صورت (b=f(a نشان میدهیم.
حال همه چیز برای ارائه تعریفی دقیق از تابع آماده است.
بحث رسمی و تعریف دقیق تابع
- تعریف
- یک تابع از مجموعه X به مجموعه Y رابطهای چون f از مجموعه X به مجموعه Y است که دارای شرایط زیر باشد:
- دامنه f مجموعه X باشد، یعنی domf=X.
- برای هر x∈X عنصر یگانه y∈Y موجود باشد که x,y)∈f) یا به عبارتی هیچ دو زوج مرتب متمایزی متعلق به f دارای مولفه اول یکسان نباشند. شرط یگانگی را به طور صریح میتوان یه این صورت فرمول بندی کرد که اگر x,y)∈f) و x,z)∈f) آنگاه y=z.
رابطهای را که دارای چنین شرایطی باشد، تابع خوش تعریف میگوییم.
برای هر x∈X یگانه عضو y در Y که به ازای آن x,y)∈f) را با (f(x نشان میدهیم. در مورد تابع این علامت گذاری، سایر علامت گذاریهایی را که در مورد روابط کلی تر استفاده میشوند چون x,y)∈f) یا xfy را متروک ساخته است. از این پس اگر f یک تابع باشد، بجای x,y)∈f) یا xfy مینویسیم (y=f(x. عضو y را مقدار تابع به ازای متغیر یا شناسه x، یا تصویر x تحت f میگوییم و نیز x را پیش نگاره y میگوییم.
کلمات نگاشت، تبدیل، تناظر و یا عملگر نیز برخی از انبوه کلماتی هستند که ممکن است در منابع مختلف بجای تابع بکار بروند اما این عبارات عموماً در برخی حوزهها، بر حالتهای خاصی از توابع دلالت دارند.
اگر f تابعی از مجموعه X به(در یا به توی) مجموعه Y باشد، این مطلب را به صورت سه تایی (f,X,Y) یا به طور معمول تر برای توابع با f:X→Y نشان میدهیم.
مشخص کردن تابع
برای مشخص کردن یک تابع باید دامنه و ضابطه آن را بشناسیم. منظور از ضابطه یک تابع f:X→Y، فرمول و یا دستوری است که برطبق آن برای هر x∈X، مقدار تابع f در x یعنی (f(x تعیین میشود. ضابطه تابع را میتوان به صورت یک عبارت جبری، مجموعهای از زوجهای مرتب یا یک رابطه بازگشتی مشخص کرد.
به این ترتیب برای مشخص کردن یک تابع از مجموعه X به مجموعه Y مینویسیم f:X→Y و سپس ضابطه آن را ذکر میکنیم.
البته گاهی در مواقعی که بیم ابهام نرود دامنه تابع را ذکر نمیکنند و به ذکر ضابطه تابع بسنده میکنند. مثلاً عرف بر این است که در حساب دیفرانسیل و انتگرال دامنه توابع در صورت ذکر نشدن اعداد حقیقی یا بازهای از اعداد حقیقی باشد.
دامنه و برد تابع
یک تابع f از مجموعه X به توی مجموعه Y را به عنوان نوعی رابطه از مجموعه X به Y تعریف کردیم. مفاهیم دامنه و برد همانگونه که برای روابط در حالت کلی قابل تعریفاند، به طریق اولی برای تابع f نیز قابل تعریف خواهند بود. بنا به تعریف دامنه تابع f که با domf نموده میشود، همان مجموعه X است. برد تابع f نیز مجموعه همه عناصری از Y است که تصویر عضوی از X تحت f باشند. برد تابع f را با ranf یا Imf نشان میدهیم. بنابه تعریف داریم:
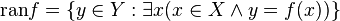
اما همانطور که در گذشته نیز اشاره شد و از تعریف فوق نیز قابل برداشت است، برد f در حالت کلی لزوماً برابر مجموعه Y نمیباشد بلکه زیرمجموعهای از آن است. برای تمایز بین مجموعه Y و برد تابع f به مجموعه Y همدامنه تابع f میگویند و آن را با codomf نشان میدهیم و بنا بر آنچه گفته شد، برد تابع زیرمجموعهای از همدامنهاش هست.
به عنوان مثال فرض کنید {X={1,2,3 و {Y={a,b,c,d و تابع f:X→Y به صورت {(f={(1,a),(2,b),(3,c تعریف شده باشد. وضوحاً دامنه این تابع مجموعه X است(میتوان برای تعیین آن مجموعه همه مولفههای اول زوجهای مرتب f را در نظر گرفت) ولی برد آن بنابه تعریف مجموعه {a,b,c} است که آشکارا زیرمجموعه حقیقی Y است.(یعنی زیرمجموعه آن است ولی با آن برابر نمیباشد)
در حقیقت برد تابع f مجموعه همه مولفههای دوم زوج مرتبهای f است. مجموعه همه عناصری از Y که به ازای یکx∈X داشته باشیم (y=f(x.
[ویرایش] تساوی دو تابع
فرض کنید f:X→Y و g:Z→W دو تابع باشند. در این صورت تساوی دو تابع f و g را چگونه میتوان تعریف کرد؟ وضوحاً تساوی f=g، تساوی بین دو مجموعه است و لذا f=g اگر و فقط اگر اعضای f و g یکسان باشند.
این مطلب بسیار موجز است و میتوان تفسیر زیبایی برای آن انجام داد. این مطلب در درجه اول ایجاب میکند که دامنه دو تابع f و g برابر باشند یعنی X=Z. چرا که برای هر x∈X ،x اگر و فقط اگر x,f(x))∈f) و چون f=g اگر و فقط اگر x,f(x))∈g) و این اگر و فقط اگر x∈Z پس X=Z. پس اولین شرط لازم برای تساوی دو تابع تساوی دامنه آنها است.
حال دو تابع f:X→Y و g:X→Z باهم برابرند، یعنی f=g اگر و فقط اگر برای هر x∈X داشته باشیم(f(x)=g(x. به عبارت دیگر اگر f=g در این صورت برای هر x∈X دلخواه و از این پس ثابت، داریم x,f(x))∈f) و چون f=g پس
x,f(x))∈g) و این یعنی (f(x)=g(x. بلعکس فرض میکنیم برای هر x∈X داشته باشیم(f(x)=g(x در این صورت، برای هر (x,y)∈f ،(x,y) اگر وفقط اگر (y=f(x و این اگر و فقط اگر (y=g(x پس x,y)∈g) و این یعنی f=g.
بنابر آنچه گفته شد دو تابع f,g باهم برابرند اگر وفقط اگر دامنهشان با هم برابر باشد و برای هر x از دامنه مشترکشان، (f(x)=g(x.
به عنوان مثال دو تابع  و g(x) = | x | با دامنه اعداد حقیقی باهم برابرند. چرا که اولاً دامنه هر دو آنها اعداد حقیقی R است و برای هر x∈R داریم:
و g(x) = | x | با دامنه اعداد حقیقی باهم برابرند. چرا که اولاً دامنه هر دو آنها اعداد حقیقی R است و برای هر x∈R داریم:

[ویرایش] تحدید و توسیع
فرض کنید f:X→Y یک تابع و A زیرمجموعهای از X باشد. در این صورت یک روش برای ساختن تابعی چون g از مجموعه A به مجموعه Y این است که برای هر g(x)،x∈A را مساوی (f(x تعریف کنیم. یعنی تابع g:A→Y با ضابطه (g(x)=f(x. بر خواننده است که خوش تعریفی این تابع را تحقیق کند. ممکن است راه دیگری نیز برای بیان این مطلب بیابیم و آن این است که دامنه تابع f را به زیرمجموعه A از X تقلیل دهیم. در این صورت تابعی خواهیم داشت که این بار نه بر روی همه اعضای X بلکه فقط بر روی عناصر زیرمجموعه خاصی از X یعنی A اثر میکند و لذا دامنه آن از X به A تغییر مییابد. چنین تابعی را که همان g است تحدید تابع f به مجموعه A میگوییم و آن را با f|A یا f|A نشان میدهیم. با این نمادگذاری داریم g=f|A. همچنین تابع f را توسیع تابع g به مجموعه X میگوییم.
بنابراین مفاهیم تحدید و توسیع دو مفهوم متقابل به هم میباشند. تحدید یک تابع به زیرمجموعهای از دامنه خود همواره یک تابع است اما توسیع دامنه یک تابع به یک مجموعه جدید که دامنه تابع قبل زیرمجموعهای از آن است همواره تابع نمیباشد ولذا در مورد توسیع توابع احتیاط بیشتری لازم است. به طور کلی اگر f:A→Y یک تابع باشد توسیع تابع f به مجموعه X تابعی چون g با دامنه X است، به طوری که تحدید g به مجموعه A برابر تابع f باشد یعنی g|A=f.
هچنین میتوان همدامنه یک تابع را نیز تحدید کرد البته در این کار احتیاط لازم است، چراکه نباید اعضایی را که متعلق به برد تابع است را حذف نمود. اما اگر f:X→Y یک تابع باشد، با تحدید Y به (f(X که همان برد تابع f است میتوان تابع (f:X→f(X را تشکیل داد که خواهید دید پوشا نیز هست.
[ویرایش] تصویر و تصویر معکوس
اگر f:X→Y یک تابع و A زیرمجموعهای از X باشد، ممکن است بخواهیم مجوعهای را در نظر بگیریم که عناصر آن تصویر عناصر A تحت f میباشند. یعنی مجموعهای که از تاثیر تابع f روی هر عضو مجموعه A حاصل میشود. چنین مجموعهای را تصویر یا نگاره A تحت تابع f میگوییم و آن را با (f(A نشان میدهیم و به این صورت تعریف میکنیم:

بنابر این (y∈f(A اگر وفقط اگر به ازای y= f(x)،x∈A یا به بیان نمادین:
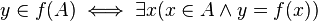
به عنوان مثال اگر {X={1,2,3,4,5 و {Y={a,b,c,d,e و f:X→Y به صورت:
- {(f={(1,a),(2,b),(3,c),(4,d),(5,d
تعریف شود و زیرمجموعه A از X به صورت {A={1,3,4 در نظر گرفته شود در این صورت:
- {f(A)={f(1),f(3),f(4)}={a,c,d
حال چون X نیز یک زیرمجموعهای از خودش است میتوان (f(X را نیز تشکیل داد، که در این صورت بنا به تعریف داریم:

که عبارت است از مجموعه همه عناصری از Y است که تصویر عضوی از X تحت f باشند که بنابه تعریف همان برد تابع f یعنی ranf است. به این ترتیب برد f را میتوان تصویر X تحت تابع f تعریف کرد.
- قضیه
- اگر f:X→Y یک تابع باشد آنگاه:


- اگر
 آنگاه
آنگاه 
قضایای فوق به سادگی از تعاریف قابل اثبات میباشند. همچنین فرض کنید  خانوادهای از زیرمجوعههای X باشد. در این صورت:
خانوادهای از زیرمجوعههای X باشد. در این صورت:


حال فرض کنید f:X→Y یک تابع باشد و B زیرمجموعهای از مجموعه Y باشد. ممکن است بخواهیم مجموعه همه اعضایی از X را تعیین کنیم که تصویر آنها تحت f عضوی از B باشد.(به شباهت این مطلب با تصویرها توجه کنید) چنین مجموعه ای را با (f-1(B نشان میدهیم و آن را تصویر معکوس یا پیشنگاره B تحت تابع f میگوییم. و بنابه تعریف داریم:

پس:

به عنوان مثال اگر {X={1,2,3,4,5 و {Y={a,b,c,d,e و f:X→Y به صورت:
- {(f={(1,a),(2,b),(3,c),(4,d),(5,d
تعریف شود و زیرمجموعه B از Y به صورت {A={a,c,e در نظر گرفته شود در این صورت:
- {f-1(B)={1,3
مشاهده میکنید که برای عضو e از B عضوی از X وجود ندارد که تصویر آن تحت f برابر e باشد. در حقیقت میتوان دید که تصویر معکوس B همواره ناتهی نیست، و تنها زمانی ناتهی است که اشتراک B با برد تابع f یعنی (f(X ناتهی باشد.
همچنین وضوحاً Y نیز زیرمجموعهای از خودش است، اگر (f-1(Y را بیابیم خواهیم داشت:

که وضوحاً از تعریف تابع این مجموعه برابر X است. پس همواره f-1(Y)=X.
- قضیه
- اگر f:X→Y یک تابع باشد آنگاه:

- اگر
 آنگاه
آنگاه 
- اگر B,C زیرمجموعههایی از Y باشند آنگاه:
- f − 1(C − B) = f − 1(C) − f − 1(B)
همچنین فرض کنید  خانواده ای زیرمجوعههای Y باشند. در این صورت:
خانواده ای زیرمجوعههای Y باشند. در این صورت:


[ویرایش] اجتماع توابع-توابع چند ضابطهای
بسیار اتفاق میافتند که مقدار یک تابع در سراسر دامنهاش با یک ضابطه مشخص نمیشود مثلاً ممکن است دامنه تابع f که آن را X مینامیم را به n مجموعه X1,X2,X3,...,Xn افراز کنیم و تابع f با دامنه X را برای هر x∈Xi به صورت (f(x)=fi(x تعریف کنیم که در آن fi تابعی با دامنه Xi است. همچنین در این صورت میتوان تابع f را برای هر x از دامنه به صورت زیر نوشت:
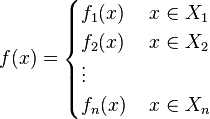
در این صورت f را تابعی با n ضابطه میگوییم.
در مثالی دیگر فرض کنید f:X→Y و g:Z→W دو تابع باشند که برای هر x متعلق به اشتراک X و Y (اشتراک دامنه f,g) داشته باشیم (f(x)=g(x. در این صورت تابع  اجتماع دو تابع f,g را به صورت زیر تعریف می کنیم:
اجتماع دو تابع f,g را به صورت زیر تعریف می کنیم:
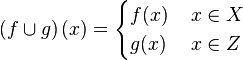
برخواننده است که خوش تعریفی این تابع را تحقیق کند. این مفهوم را میتوان گسترش داد یعنی اگر  خانوادهای از مجموعههای دو به دو جدا از هم باشد و برای هر fi,i∈I تابعی با دامنه Ai باشد، میتوان تابع f، اجتماع توابع fi برای هر i∈I را با دامنه
خانوادهای از مجموعههای دو به دو جدا از هم باشد و برای هر fi,i∈I تابعی با دامنه Ai باشد، میتوان تابع f، اجتماع توابع fi برای هر i∈I را با دامنه  را به صورت برای هر x از دامنه به صورت
را به صورت برای هر x از دامنه به صورت
(f(x)=fi(x اگر x∈Ai تعریف کرد. در ادامه نمونههایی از توابع چند ضابطهای را خواهید دید.
[ویرایش] نمودار تابع

شکل(3) نمودار پیکانی یک تابع
منظور از نمودار یک تابع f:X→Y به تصویر کشیدن تناظری است که f بین دو مجوعه X و Y ایجاد میکند. برای این کار برای همه روابط و بلاخص توابع عموماً از نمودار پیکانی استفاده میشود. برای رسم نمودار پیکانی تابع f:X→Y، دو منحنی بسته، نظیر آنچه در نمودار ون استفاده میشود را برای نمایش مجموعه X و Y انتخاب میکنیم و عناصر هر یک را بوسیله نقاطی در آنها مشخص میکنیم. سپس بین هر عضو x∈X و (f(x یک پیکان از x به (f(x به نشانه تناظر بین آن دو رسم میکنیم. به عنوان مثال اگر {X={1,2,3,4,5 و {Y={a,b,c,d,e و f:X→Y به صورت {(f={(1,a),(2,b),(3,c),(4,d),(5,d تعریف شده باشد نمودار پیکانی آن به صورت مقابل است.

شکل (4) نمونهای از نمودار یک تابع حقیقی در دستگاه مختصات دکارتی
این روش گرچه مناسب است ولی برای نمایش همه توابع بویژه توابعی با دامنه اعداد حقیقی(و به طور کلی توابعی که عددی هستند) چندان کاربرد ندارد. اگر f تابعی با دامنه اعداد حقیقی R باشد آن را تابع حقیقی میگوییم و برای نمایش نمودار آن از دستگاه مختصات دکارتی استفاده میکنیم و روش کار به این صورت است که برای هر x∈R زوج مرتب ((x,f(x) که نماینده نقطهای در صفحه دکارتی است را رسم میکنیم و به این ترتیب نمودار تابع f حاصل میشود. رسم نمودار تابع، باعث میشود دیدی کلی نسبت به آن تابع پیدا کنیم و همچنین بسیاری از خواص مربوط به توابع بویژه توابع حقیقی مانند پیوستگی، مشتق پذیری، نقاط بحرانی و عطف، صعودی یا نزولی بودن و... از روی نمودار آنها قابل تعیین است. به عنوان مثال با بررسی شکل(4) میتوان گفت این تابع در چه بازههایی صعودی و در چه بازههایی نزولی است، این تابع در سراسر دامنه خود پیوسته و مشتق پذیر است، دارای دو نقطه بحرانی و یک نقطه عطف است و ... .
همچنین از روی نمودار یک رابطه میتوان تابع بودن آن را بررسی کرد. به عنوان مثال نمودار شکل(1) معرف یک تابع نمیباشد چون عضو 3 به دو مقدار متناظر شده است. همچنین در نمودار رسم شده در دستگاه دکارتی در شکل مقابل، وضوحاً برای هر عدد حقیقی مثبت x تابع دارای دو مقدار است. به طور کلی یک نمودار در دستگاه مختصات دکارتی یک تابع است اگر هر خط عمودی مرسوم بر محور x ها نمودار را حداکثر در یک نقطه قطع کند.
[ویرایش] تابع یک به یک و پوشا
فرض کنید f:X→Y یک تابع باشد. در اینصورت برای تناظری که بین اعضای X و Y بوسیله تابع f برقرار میشود حالات مختلفی را میتوان تصور کرد.
اولین حالت اینکه ممکن است به ازای هر y متعلق به برد تابع f، تنها یک x در دامنه موجود باشد که (y=f(x. این شرط را میتوان چنین فرمول بندی کرد که اگر به ازای x1,x2∈X داشته باشیم (f(x1)=f(x2 آنگاه x1=x2 یا:

چنین تابعی را با این ویژگی یک تابع یک به یک(تک گزین) یا انژکتیو میگوییم. یک به یک بودن تابع f را گاهی برای اختصار با نماد 1-1 نشان میدهند. در چنین حالتی ضمن اینکه بدلیل تابع بودن f هیچ دو زوج مرتبی از f دارای مولفه اول یکسان نمیباشند، به دلیل یک به یک بودن هیچ دو زوج مرتبی از f دارای مولفه دوم یکسان نیز نمیباشند.
به عنوان مثال f:R→Rبه ضابطه f(x)=x2 یک به یک نمیباشد چرا که اگر (f(x1)=f(x2 در این صورت x12=x22 اما الزاماً این نتیجه نمیدهد x1=x2 پس تابع یک به یک نمیباشد.
یک به یک بودن یک تابع از روی نمودار تابع نیز قابل بررسی است. در نمودار پیکانی تابع یک به یک f، وضوحاً به هر عضو از همدامنه f انتهای حداکثر یک پیکان وارد شده است. به این ترتیب نمودار پیکانی شکل(2) نمایش گر یک تابع غیر یک به یک است. همچنین نمودار یک تابع حقیقی یک به یک به گونهای است که هر خط موازی محور x ها، نمودار آن را حداکثر در یک نقطه قطع میکند. به این ترتیب نمودار شکل(4) مربوط به تابعی غیر یک به یک است.
همانطور که در گذشته نیز اشاره شد در تابع f:X→Y برد f ممکن است دقیقاً برابر مجموعه Y نباشد، ولی همواره زیرمجموعهای از Y است.
حال اگر برد تابع f برابر مجموعه Y باشد یعنی ranf=Y در این صورت هر عضو Y تصویر یک عضو مجموعه X تحت f خواهد بود. یعنی برای هر y∈Y، عضوی چون x∈X وجود دارد که (y=f(x. در این حالت تابع f:X→Y را تابع پوشا(برو) یا سوژکتیو میگویند و به اصطلاح میگویند f مجموعه X را بروی Y مینگارد.
این نکته بسیار حایز اهمیت است، چرا که در مورد نماد f:X→Y دو عبارت f تابعی از X به توی Y است و f تابعی از X به روی Y است با هم تفاوت دارند و عبارت دوم چیزی بیش از عبارت اول یعنی پوشا بودن تابع f را نیز بیان میکند.
پس تابع f:X→Y یک تابع پوشا(برو) است هرگاه:

اگر f:X→Y یک تابع غیر پوشا باشد، یک راه برای پوشا کردن تابع f تحدید همدامنه آن به برد f است. به عبارت دیگر میتوان اعضایی از مجموعه Y(همدامنه) که تصویر هیچ عضوی از X نمیباشند(یعنی متعلق به برد تابع نمیباشند) را حذف نمود در این صورت تابع f از X به مجموعه تقلیل داده شده تابعی پوشا خواهد بود. مجموعهای که میتوان Yرا به آن تحدید نمود و تابعی پوشا بدست آور تصویر X تحت f با همان (f(X است که همانطور که در بالا نیز اشاره شد، این مجموعه همان برد تابع است.
بنابر این اگر f:X→Y یک تابع باشد تابع (f:X→f(X تابعی پوشا است و این از تعریف (f(X قابل اثبات است. به عنوان مثال f:R→Rبه ضابطه f(x)=x2 یک تابع پوشا نمیباشد. چرا که اعداد حقیقی منفی در همدامنه f(همان مجموعه R) تصویر هیچ عضوی از دامنه خود نمیباشند، چرا که مربع هیچ عدد حقیقی منفی نیست. اما تابع f:R→R≥0 یک تابع پوشا است چون برای هر y∈R میتوان قرار داد  و داریم
و داریم  و لذا f پوشا است.
و لذا f پوشا است.

شکل(8) نمونهای از یک تابع دوسویی
حال که با مفاهیم یک به یک بودن و پوشا بودن آشنا شدیم وضوحاً یک تابع نسبت به دارای بودن این خواص میتواند چهار حالت مختلف باشد. یک حالت جالب توجه و بسیار مهم زمانی است که یک تابع هم یک به یک و هم پوشا باشد. چنین تابعی را تناظر یک به یک یا دو سویی یا بیژکتیو میگوییم.
به عنوان مثال تابع f(x)=x3 بر مجموعه اعداد حقیقی یک تناظر یک به یک است.
از نمودار پیکانی مقابل میتوانید ببینید که چنین تابعی دارای چه ویژگی خاصی است. وجود چنین تابعی بین دو مجموعه متناهی ایجاب میکند تعداد اعضای آنها با هم برابر باشد. این مطلب در حالت کلی نیز درست است. یعنی اگر تابعی دوسویی بین دو مجموعه(خواه متناهی یا غیرمتناهی) برقرار باشد عدد اصلی آن دو مجموعه با هم برابر است.
از توابع دوسویی برای بسیاری از تعاریف در نظریه مجموعهها مثلاً تشابه مجموعههای خوشترتیب یا تعریف همتوانی دو مجموعه استفاده میشود.
[ویرایش] مجموعه توابع
اگر X و Y دو مجوعه باشند مجموعه همه توابع از مجموعه X به مجموعه Y را با YX نشان میدهیم و بنابه تعریف داریم:
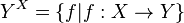
عدد اصلی این مجموعه را نیز میتوان به صورت زیر بدست آورد(برای اثبات به مقاله حساب اعداد اصلی رجوع کنید.):
- card(YX) = (cardY)cardX
از رابطه فوق نتیجه میشود اگر X مجوعهای n عضوی و Y مجموعهای m عضوی باشد تعداد توابع قابل تعریف از مجوعه X به مجموعه Y برابر است با mn که البته برای اثبات این مسئله خاص راه حل ترکیباتی هم وجود دارد. توضیح اینکه اگر بخواهیم تابع f:X→Y را تعریف کنیم هر عضو از n عضو مجموعه X چون x∈X، را میتوان به m طریق به یک عضو از مجموعه Y نسبت داد. پس بنا بر اصل شمارش تعریف چنین تابعی به mn طریق ممکن خواهد بود.
حال فرض کنید f:X→Y یک تابع باشد و X مجموعهای n عضوی و Y مجموعهای m عضوی باشند.
در این صورت اگر m≥n میتوان f را به صورت تابعی یک به یک بین دو مجموعه X و Y تعریف کرد. برای این کار کافی است n عضو را از بین m عضو مجموعه Y انتخاب کنیم و بیاد داشته باشید که ترتیب انتخاب اعضا نیز مهم است و لذا تعداد توابع یک به یک قابل تعریف برابر است با جایگشت n شی از m شی که برابر است با:

همچنین اگر n≥m، میتوان f را به صورت تابعی پوشا نیز تعریف کرد که تعداد توابع پوشا از مجموعه X به مجموعه Y برابر است با:

که البته اثبات آن بوسیله اصل شمول و عدم شمول انجام پذیر است و بدلیل طولانی بودن از ارائه برهان آن خودداری میکنیم. همچنین تعداد توابع دوسویی روی مجوعه n عضوی X برابر است با !n.
[ویرایش] ترکیب توابع

شکل(9) نمودار ترکیب دو تابع
فرض کنید g:X→Y و f:Y→Z دو تابع باشند. در این صورت برای هر x∈X، داریم g(x)∈Y و لذا (g(x در دامنه تابع f قرار میگیرد و لذا
f(g(x))∈Z. کاری که انجام دادیم این بود که ابتدا x∈X را توسط تابع g به عضوی از مجموعه Y متناظر کردیم و عضو حاصله در Y را بوسیله تابع f به عضوی از مجموعه Z متناظر کردیم. به این ترتیب میتوان گفت عضو x را توسط دو تابع g,f به عضوی از مجموعه Z متناظر کردیم. این کار را میتوان به طور مستقیم نیز انجام داد.
برای این منظور تابع h:X→Z را برای هر x متعلق به مجموعه X، به صورت ((h(x)=f(g(x تعریف میکنیم. چنین تابعی را ترکیب تابع g و f میگوییم و آن را با fog (بخوانید f اُ g) نشان میدهیم.
با توجه به آنچه بیان شد تابع fog را میتوان به صورت زیر نیز تعریف کرد:

توجه داشته باشید که در حالت کلی ترکیب توابع جابجایی نمیباشد یعنی همواره رابطه fog=gof برقرار نمیباشد.
به عنوان مثال اگر f:R→R با ضابطه f(x)=x3 و g:R→R باضابطه g(x)=lnx باشد در این صورت، داریم:
- (fog)(x) = f(g(x)) = f(lnx) = (lnx)3
- (gof)(x) = g(f(x)) = g(x3) = ln(x)3 = 3lnx
- قضیه
- ترکیب توابع شرکت پذیر است، یعنی اگر f:A→B,g:B→C,h:C→D سه تابع باشند آنگاه ho(gof)=(hog)of.
برای اثبات توجه میکنیم که هر دوی ho(gof),(hog)of توابعی از مجموعه A به توی مجموعه D میباشند و برای هر x∈A داریم:
- (((ho(gof))(x)=h(g(f(x)
و
- (((hog)of)(x)=h(g(f(x))
که این تساوی را توجیه میکند.
[ویرایش] معکوس تابع
یادآور میشویم که اگر R یک رابطه از مجموعه X به مجموعه Y باشد، آنگاه معکوس رابطه R را با R-1 نشان میدهیم که عبارت است از:

و این یک رابطه از مجموعه Y به مجموعه X است. حال تابع f:X→Y نیز یک رابطه است و لذا به معکوس آن را نیز میتوان تعریف کرد که آن را با f-1 نشان میدهیم و حداقل یک رابطه از Y به X است.

حال این سوال مطح میشود که آیا f-1 نیز یک تابع خواهد بود و یا چه هنگامی f-1 یک تابع است؟
وضوحاً برای اینکه f-1:Y→X تابع باشد، باید در شرایط تابع بودن(که در گذشته بیان شد) صدق کند یعنی در درجه اول دامنهاش همان مجموعه Y باشد و نیز هر عضو Y را به عضوی یگانه از X تصویر کند.
اما برای اینکه دامنه f-1 برابر مجموعه Y باشد، برد تابع f باید برابر مجموعه Y باشد و این یعنی تابع f باید پوشا باشد.
برای اینکه f-1 هر عضو از دامنه خود Y را به یک عضو یگانه از مجموعه X تصویر کند، باید برای هر x1,x2∈X داشته باشیم اگر (f(x1)=f(x2 آنگاه x1=x2 و این یعنی f باید تابعی یک به یک باشد.
بنابراین معکوس تابع f:X→Y یعنی f-1 تابعی از Y به X خواهد بود اگر وفقط اگر f:X→Y یک دوسویی باشد. در این حالت f-1:Y→X را تابع معکوس تابع f میگوییم.
اگر f-1 معکوس تابع f:X→Y باشد رابطه زیر را بین دامنه و برد f و f-1 داریم:
- domf − 1 = ranf
- ranf − 1 = domf
همچنین اگر (y=f(x پس x,y)∈f) ولذا y,x)∈f-1) پس (x=f-1(y و بلعکس.
رابطه بین یک تابع و معکوسش را میتوان به این صورت توصیف کرد که تابع f-1 معکوس تابع f، دقیقاً عکس تناظری که تابع f بیانگر آن است را توصیف میکند. به همین دلیل و بنابه تعریف تابع معکوس نمودار پیکانی تابع f-1 معکوس تابع f:X→Y با معکوس کردن جهت فلشها بدست میآید.
همچنین اگر f تابعی حقیقی باشد، برای اینکه نمودار معکوس f را تعیین کنیم کافی است قرینه نمودار تابع f را نسبت به نیمساز ربع اول و سوم یعنی f(x)=x رسم کنیم و چون انعکاس نسبت به نیمساز ربع اول و سوم موجب جابجایی مولفههای اول و دوم زوجهای مرتب تابع f میشود و این در حقیقت همان هدف ماست.
حال اگر f:X→Y تابعی یک به یک و پوشا با معکوس f-1:Y→X باشد، برای هر x∈X داریم:
- (fof − 1)(x) = f(f − 1)(x) = x
- (f − 1of)(x) = f − 1(f(x)) = x
و این یعنی ترکیب هر تابع با معکوس خودش برابر با تابع همانی است.
[ویرایش] بررسی چند تابع خاص
فرض کنید X و Y دو مجموعه ناتهی و b∈Y عضوی ثابت و لخواه باشد. در این صورت میتوان تابع f:X→Y را با ضابطه برای هر f(x)=b,x∈X تعریف کرد که به آن تابع ثابت میگوییم. وجه تسمیه این تابع نیز واضح است، چرا که به هر عضو دلخواه مجموعه X عضو ثابت b از مجموعه Y را نسبت میدهد. این تابع را معمولاً با Cb نشان میدهیم و میتوان به آن را صورت زیر نیز نشان داد:

نمودار یک تابع ثابت روی اعداد حقیقی یک خط موازی محور Xها خواهد بود.
[ویرایش] تابع همانی
فرض کنید X یک مجموعه ناتهی باشد. در این صورت بدیهیترین رابطهای که ممکن است روی مجموعه X تعریف کنیم رابطه همانی با انعکاسی است. اگر این رابطه را با I نشان دهیم داریم:


شکل(10) نمودار تابع همانی روی مجموعه اعداد حقیقی
به سادگی میتوان دید رابطه همانی روی مجموعه X یک تابع از X به روی خودش است که به آن تابع همانی میگوییم. به عبارت دیگر I:X→X با ضابطه برای هر I(x)=x،x∈X تابع همانی است. اگر مجموعه X را مجموعه اعداد حقیقی R در نظر بگیریم، تابع همانی از مجموعه R به روی مجموعه R تابع f(x)=x است که همان نیمساز ربع اول و سوم دستگاه مختصات دکارتی است. به سادگی میتوان تحقیق کرد این تابع در مجموعه اعداد حقیقی دوسویی است.
حال مجموعه ناتهی X و زیرمجموعه A از آن را در نظر بگیرید. در این صورت بنابه آنچه از قبل گفته شد میتوان دامنه تابع همانی روی X یعنی I:X→X را مجموعه A تحدید نمود و حاصل تابع I|A:A→X است با ضابطه برای هر I(x)=x،x∈A، این تابع را که زیرمجموعه A از X را به توی X مینگارد را تعمیمی بر تابع همانی میتوان دانست که به آن تابع احتوا یا شمول میگویند.
قدر مطلق اعداد حقیقی را میتوان به عنوان یک تابع در نظر گرفت. این تابع را میتوان به صورت f:R→R تعریف کرد:

قدر مطلق x را معمولا با |x| نشان میدهیم. وضوحاً این تابع یک تابع از مجموعه اعداد حقیقی به روی مجموعه اعداد حقیقی نامنفی است.
تابع sgn:R→R را با ضابطه:

تابع علامت میگویم. نماد sgn کوتاه نوشتی برای sign به معنی علامت است. وجه تسمیه این تابع نیز واضح است، چرا که اعداد را بر حسب علامتشان جدا میکند. این تابع نمونهای از توابع چند ضابطهای است.
برای مطالعه بیشتر به مقالات تابع انتخاب و اصل انتخاب مراجعه کنید.
در نظریه اصل موضوعی مجموعهها اصلی موضوعی موسوم به اصل موضوع انتخاب بیان میکند برای هر دسته ناتهی  از مجموعههای ناتهی، تابعی چون
از مجموعههای ناتهی، تابعی چون  وجود دارد که بری هر
وجود دارد که بری هر  داریم
داریم  این تابع را تابع انتخاب میگوییم.
این تابع را تابع انتخاب میگوییم.
اجمالاً تابع انتخاب، انتخابهای همزمان از اعضای دسته  انجام میدهد و اعضای انتخاب شده را در برد خود قرار میدهد.
انجام میدهد و اعضای انتخاب شده را در برد خود قرار میدهد.
نکتهای که جالب و جنجال بر انگیز است این است که تنها وجود این تابع بوسیله اصل موضوع انتخاب تضمین میشود حتی اگر تعداد مجموعههای دسته مفروض  نامتناهی باشد، و هیچ روشی برای نحوه این انتخاب ارائه نمیکند به عبارت دیگر برای این تابع ضابطهای در نظر نمیگیرد. این تابع به ما امکان انتخابهای نامتناهی را هم میدهد که این امر برای اثبات بسیاری از قضایای نظریه مجموعهها، خصوصاً قضیه خوشترتیبی و لم زرن لازم است.
نامتناهی باشد، و هیچ روشی برای نحوه این انتخاب ارائه نمیکند به عبارت دیگر برای این تابع ضابطهای در نظر نمیگیرد. این تابع به ما امکان انتخابهای نامتناهی را هم میدهد که این امر برای اثبات بسیاری از قضایای نظریه مجموعهها، خصوصاً قضیه خوشترتیبی و لم زرن لازم است.
[ویرایش] تابع مشخصه

شکل(11) نمودار پیکانی تابع مشخصه A در X
فرض کنید X مجموعهای ناتهی و A زیرمجموعهای از X باشد. در این صورت تابع مشخصه A در X، یعنی  (بخوانید خی A) را برای هر x∈X به صورت زیر تعریف میکنیم:
(بخوانید خی A) را برای هر x∈X به صورت زیر تعریف میکنیم:

البته انتخاب مجموعه {0,1} هر چند معمولتر است ولی الزامی نیست و میتوان هر مجموعه دو عضوی دیگر را نیز انتخاب کرد. این تابع به هر عضو مجموعه A عدد یک و به هر عضو X-A یعنی عناصری که متعلق به X هستند ولی به A تعلق ندارند مقدار صفر رانسبت میدهد. وجه تسمیه این تابع این است که عناصری زیرمجموعه A از X را از سایر عناصری که در A قرار ندارند جدا میکند.
نمونهای از یک تابع مشخصه معروف تابع دیریکله است که همان تابع مشخصه Q(اعداد گویا) در R(اعداد حقیقی) است که آن را با D نشان میدهیم و به این صورت تعریف میکنیم:
-

به سادگی میتوان نشان داد این تابع هر هیچ نقطه از دامنه خود پیوسته نمیباشد.
[ویرایش] توابع دو (یا چند) متغیره
عباراتی چون f(x,y) = sin(xy) یا f(x,y,z) = x2 + y2 + z2 را در نظر بگیرید. هر یک از آنها دو یا بیش از دو متغییر از دامنه میپذیرند و یک مقدار یگانه را به همه آنها نسبت میدهند. گاهی ممکن است تابع بجای یک شناسه دو یا چند شناسه را به بپذیر و آنها را به یک عضو از برد خود نسبت دهد، در این صورت تابع را دو یا چند متغیره میگوییم. چنین توابعی رابطهای بین بیش از دو مجموعه هستند. به عنوان مثال تابع اول را میتوان تابعی به صورت f:R×R→R توصیف کرد که در این صورت تابع زوج (x,y) را به عنوان شناسه خود میپذیرد و آن را به عضوی از R نسبت میدهد که در این صورت اعضای تابع f را میتوان به صورت سه تایی ((x,y,f(x,y) نشان داد.
برای مطالعه بیستر به مقاله عمل دوتایی مراجعه کنید.
نمونه ای از پرکاربرد ترین توابع چند متغیره، عمل دوتایی است. یک عمل دوتایی روی مجموعه A تابعی است چون f:A×A→A که به هر عضو (a1,a2) از A×A عضو یگانهای چون f(a1,a2)=a3 را نسبت میدهد.
اعمال سادهای چون جمع و ضرب اعداد نمونهای از دو عمل دوتایی هستند. چنین تابعی دو عضو(نه لزوماً متمایز) از مجموعه A را دریافت میکند و آن را به عضوی دیگر از مجموعه A نسبت میدهد. این خود نوعی ترکیب یا عمل روی اعضا را در ذهن تداعی میکند. در مورد یک عمل دوتایی برای نماشی بهتر از نمادگذاری خاصی استفاده میشود. یک عمل دوتایی روی مجموعه A را معمولاً با *,° و گاهی با نمادهای + و . نشان میدهیم. در این صورت عمل دو تایی روی مجموعه A تابعی چون A×A→A:* خواهد بود. همچنین حاصل تابع * را به ازای (a1,a2) از A×A بجای (a1,a2)* با a1*a2 نشان میدهیم.
برای مطالعه بیستر به مقاله دنباله مراجعه کنید.
هر دنباله تابعی با دامنه اعداد طبیعی چون  که A مجموعهای دلخواه است. یک دنباله صرفاً اعضای A را بوسیله اعداد طبیعی شماره گذاری میکند پس در مورد یک دنباله آنچه مهم است معمولاً برد دنباله است و اعداد طبیعی صرفاً جهت شماره گذاری یا اندیس گذاری استفاده میشوند. در این حالت است که نمادگذاری دچار تغییر میشود. برای هر عدد طبیعی n، مقدار دنباله f را در n بجای (f(n با fn نشان میدهیم و به آن جمله nام دنباله میگوییم. خود دنباله را با {fn} نشان میدهیم. دنباله نیز به عنوان یک تابع دارای ضابطه است که به آن جمله عمومی دنباله میگوییم.
که A مجموعهای دلخواه است. یک دنباله صرفاً اعضای A را بوسیله اعداد طبیعی شماره گذاری میکند پس در مورد یک دنباله آنچه مهم است معمولاً برد دنباله است و اعداد طبیعی صرفاً جهت شماره گذاری یا اندیس گذاری استفاده میشوند. در این حالت است که نمادگذاری دچار تغییر میشود. برای هر عدد طبیعی n، مقدار دنباله f را در n بجای (f(n با fn نشان میدهیم و به آن جمله nام دنباله میگوییم. خود دنباله را با {fn} نشان میدهیم. دنباله نیز به عنوان یک تابع دارای ضابطه است که به آن جمله عمومی دنباله میگوییم.
[ویرایش] توابع حقیقی و مختلط
هر تابع با دامنه اعداد حقیقی را یک تابع حقیقی میگوییم. حساب دیفرانسیل و انتگرال بخشی از ریاضیات است که بر اساس توابع حقیقی شکل گرفته است و به مطالعه توابع حقیقی و خواص آنها میپردازد که البته در این بین توابعی حقیقی پیوسته و مشتق پذیر از اهمیت بیشتری برخوردارند چرا که نوعی خوشرفتاری در آنها دیده میشود. منظور از خوشترفتار بودن این است که رفتار آنها قابل پیشبینی بوده و از قوانین و قضایای خاصی چون قضیه مقدار میانی یا میانگین و... پیروی میکنند. چنین توابعی در اکثر بخشهای ریاضی بویژه آنالیز ریاضی و علوم کلیه مهندسی و کامپیوتری مورد استفاده قرار میگیرند.
همچنین ممکن است تابع را بر مجموعه اعداد مختلط در نظر بگیریم که در این صورت توابع حاصله را تابع مختلط میگوییم. این توابع بویژه در مطالعه هندسه فراکتالها، و علوم مهندسی چون طراحی مدارات و سیستمهای مختلف الکترنیکی و مخابراتی کاربرد بسیار فراوان دارند. همچینین در رایاضیات شاخهای از آنالیز ریاضی به نام آنالیز مختلط به بررسی این توابع میپردازد.
در زیر فهرستی بیشتر در مورد مطالب مربوط به توابع حقیقی یا مختلط مشاهده میکنید:
[ویرایش] پیشینه تابع
«تابع»، به عنوان تعریفی در ریاضیات، توسط گاتفرید لایبنیز در سال ۱۶۹۴، با هدف توصیف یک کمیت در رابطه با یک منحنی به وجود آمد، مانند شیب یک نمودار در یک نقطه خاص. امروزه به توابعی که توسط لایبنیز تعریف شدند، توابع مشتقپذیر میگوییم، اغلب افراد در هنگام آموختن ریاضی با این گونه توابع برمیخورند. در این گونه توابع افراد میتوانند در مورد حد و مشتق صحبت کنند. چنین توابعی پایه حساب دیفرانسیل و انتگرال را میسازند.
واژه تابع بعدها توسط لئونارد اویلر در قرن هجدهم، برای توصیف یک عبارت یا فرمول شامل متغیرهای گوناگون مورد استفاده قرار گرفت، مانند f(x) = sin(x) + x۳.
در طی قرن نوزدهم، ریاضیدانان شروع به فرمول بندی تمام شاخههای ریاضی براساس نظریه مجموعهها کردند. وایراشتراس بیشتر خواهان به وجود آمدن حساب دیفرانسیل و انتگرال در علم حساب بود تا در هندسه، یعنی بیشتر طرفدار تعریف اویلر بود.
در ابتدا، ایده تابع ترجیحاً محدود شد. ژوزف فوریه مدعی بود که تمام توابع از سری فوریه پیروی میکنند در حالی که امروزه هیچ ریاضیدانی این مطلب را قبول ندارد. با گسترش تعریف توابع، ریاضیدانان توانستند به مطالعه «عجایب» در ریاضی بپردازند از جمله تابعی که بوسیله وایراشتراس معرفی شد که در سراسر دامنه خود پیوسته ولی در هیچ نقطهای مشتقپذیر نبود. کشف چنین توابعی موجب شد تا توابع تنها به توابع پیوسته و مشتقپذیر محدود نشوند.
تا انتهای قرن نوزدهم ریاضیدانان سعی کردند که مباحث ریاضی را با استفاده از نظریه مجموعهها فرمولبندی کنند و آنها در هر موضوع ریاضی به دنبال تعریفی بودند که براساسنظریه مجموعهها و نتایج آن باشد. دیریکله و لوباچوسکی هر یک به طور مستقل و تصادفاً هم زمان تعریف «رسمی» از تابع ارائه دادند.
در این تعریف، یک تابع حالت خاصی از یک رابطه است که در آن برای هر مقدار اولیه یک مقدار ثانویه منحصر به فرد وجود دارد.
تعریف تابع در علم رایانه، به عنوان حالت خاصی از یک رابطه، به طور گستردهتر در منطق و علم تئوری رایانه مطالعه میشود.
[ویرایش] توابع در سایر علوم
مفهوم تابع در همه علوم کاربرد فراوان دارد. برای مثال در فیزیک، هنگامی که میخواهیم رابطه بین چند متغیر را بیان کنیم، مخصوصاً در زمانی که مقدار یک متغیر کاملاً وابسته به متغیر دیگر است. برای مثال وقتی که میخواهیم نشان دهیم که تغییر دمای آب چه تاثیری بر روی چگالی آن میگذارد.
توابع در علوم مختلف بیشتر نه به عنوان چیزی که هست، بلکه به عنوان چیزی که کاری را انجام میدهند مورد توجه هستند. در این دیدگاه توابع به عنوان عملگرهای در نظر گرفته میشوند که کاری را بر روی ورودیهای خود انجام میدهند. توابع را همچنین مورد استفاده در علم رایانه برای مدلسازی ساختمان دادهها و تاثیرات الگوریتم میبینیم.
[ویرایش] جستارهای وابسته
- Lawrence S. Husch (۲۰۰۱). Visual Calculus. University of Tennessee.
- João Pedro da Ponte (۱۹۹۲). The history of the concept of function and some educational implications. The Mathematics Educator ۳(۲), ۳-۸. available online in Microsoft Word and HTML formats.
- Anton, Howard (۱۹۸۰). Calculus with analytical geometry.. New York:John Wiley and Sons. ISBN ۰-۴۷۱-۰۳۲۴۸-۴.
- ایان استیوارت،دیوید تال. مبانی ریاضیات. ترجمهٔ محمد مهدی ابراهیمی. تهران: مرکز نشر دانشگاهی، 1376، ISBN 964-01-0253-9.
- شووینگ تی.لین و یو-فنگ. لین. نظریه مجموعهها و کاربرد آن. ترجمهٔ عمید رسولیان. تهران: مرکز نشر دانشگاهی، 1384، ISBN 964-01-0462-0.








 ، اما در عبارت دوم با قرار دادن مقدار x مقداری یگانه برای y یعنی x2 حاصل میشود. به عنوان مثال در عبارت (1) اگر x=2 آنگاه
، اما در عبارت دوم با قرار دادن مقدار x مقداری یگانه برای y یعنی x2 حاصل میشود. به عنوان مثال در عبارت (1) اگر x=2 آنگاه  اما اگر در عبارت (2) قرار دهیم x=2 تنها یک جواب y=4 را بدست میآوریم.
اما اگر در عبارت (2) قرار دهیم x=2 تنها یک جواب y=4 را بدست میآوریم.

 نشان میدهیم.
نشان میدهیم. را با ضابطه f(x)=x2 در نظر بگیرید. دامنه این تابع مجموعه اعداد حقیقی است اما آیا برد آن نیز همان مجموعه اعداد حقیقی R است؟ پاسخ آشکارا منفی است چون اعداد حقیقی منفی، چون 1- تصویر هیچ
را با ضابطه f(x)=x2 در نظر بگیرید. دامنه این تابع مجموعه اعداد حقیقی است اما آیا برد آن نیز همان مجموعه اعداد حقیقی R است؟ پاسخ آشکارا منفی است چون اعداد حقیقی منفی، چون 1- تصویر هیچ 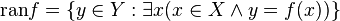
 و
و 

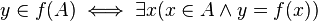



 آنگاه
آنگاه 










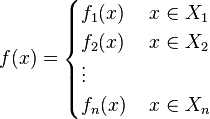
 اجتماع دو تابع f,g را به صورت زیر تعریف می کنیم:
اجتماع دو تابع f,g را به صورت زیر تعریف می کنیم: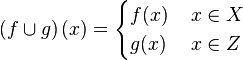
 را به صورت برای هر x از دامنه به صورت
را به صورت برای هر x از دامنه به صورت





 و داریم
و داریم  و لذا f پوشا است.
و لذا f پوشا است.
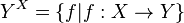











 از مجموعههای ناتهی، تابعی چون
از مجموعههای ناتهی، تابعی چون  وجود دارد که بری هر
وجود دارد که بری هر  داریم
داریم  این تابع را تابع انتخاب میگوییم.
این تابع را تابع انتخاب میگوییم.
 (بخوانید خی A) را برای هر x∈X به صورت زیر تعریف میکنیم:
(بخوانید خی A) را برای هر x∈X به صورت زیر تعریف میکنیم:

 که A مجموعهای دلخواه است. یک دنباله صرفاً اعضای A را بوسیله اعداد طبیعی شماره گذاری میکند پس در مورد یک دنباله آنچه مهم است معمولاً برد دنباله است و اعداد طبیعی صرفاً جهت شماره گذاری یا اندیس گذاری استفاده میشوند. در این حالت است که نمادگذاری دچار تغییر میشود. برای هر عدد طبیعی n، مقدار دنباله f را در n بجای (f(n با fn نشان میدهیم و به آن جمله nام دنباله میگوییم. خود دنباله را با {fn} نشان میدهیم. دنباله نیز به عنوان یک تابع دارای ضابطه است که به آن جمله عمومی دنباله میگوییم.
که A مجموعهای دلخواه است. یک دنباله صرفاً اعضای A را بوسیله اعداد طبیعی شماره گذاری میکند پس در مورد یک دنباله آنچه مهم است معمولاً برد دنباله است و اعداد طبیعی صرفاً جهت شماره گذاری یا اندیس گذاری استفاده میشوند. در این حالت است که نمادگذاری دچار تغییر میشود. برای هر عدد طبیعی n، مقدار دنباله f را در n بجای (f(n با fn نشان میدهیم و به آن جمله nام دنباله میگوییم. خود دنباله را با {fn} نشان میدهیم. دنباله نیز به عنوان یک تابع دارای ضابطه است که به آن جمله عمومی دنباله میگوییم.

 است. بر اساس قضیه حد مرکزی Sn در بی نهایت به سمت
است. بر اساس قضیه حد مرکزی Sn در بی نهایت به سمت  برگ درختان سبز در نظر هوشیار هر ورقش دفتری است معرفت کردگار
برگ درختان سبز در نظر هوشیار هر ورقش دفتری است معرفت کردگار