Involute
 |
 |
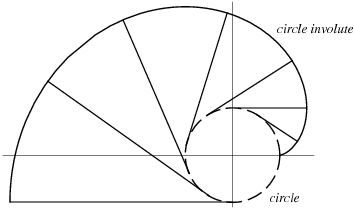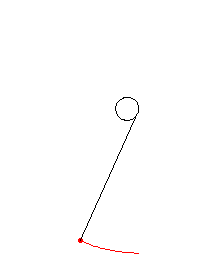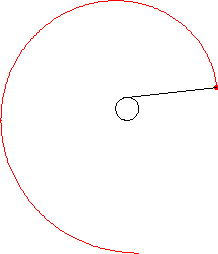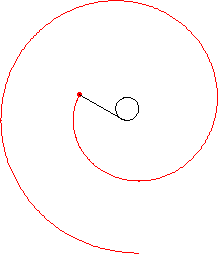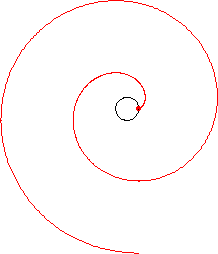
Attach a string to a point on a curve. Extend the string so that it is tangent to the curve at the point of attachment. Then wind the string up, keeping it always taut. The locus of points traced out by the end of the string is called the involute of the original curve, and the original curve is called the evolute of its involute. This process is illustrated above for a circle.
Although a curve has a unique evolute, it has infinitely many involutes corresponding to different choices of initial point. An involute can also be thought of as any curve orthogonal to all the tangents to a given curve.
The equation of the involute is
 |
(1) |
where 
is the tangent vector
 |
(2) |
and 
is the arc length
 |
(3) |
This can be written for a parametrically represented function 
as
 |
 |
 |
(4) |
 |
 |
 |
(5) |
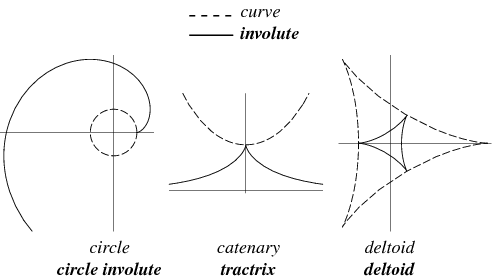
The following table lists the involutes of some common curves, some of which are illustrated above.
| curve | involute |
| astroid involute | astroid 1/2 times as large |
| cardioid involute | cardioid 3 times as large |
| catenary involute | tractrix |
| circle catacaustic | limaçon |
| circle involute | a spiral |
| cycloid involute | equal cycloid |
| deltoid involute | deltoid 1/3 times as large |
| ellipse involute | unnamed curve |
| epicycloid involute | smaller epicycloid |
| hypocycloid involute | similar hypocycloid |
| logarithmic spiral involute | another logarithmic spiral |
| nephroid involute | Cayley's sextic or nephroid 2 times as large |
| semicubical parabola involute | half a parabola |
REFERENCES:
Cundy, H. and Rollett, A. "Roulettes and Involutes." §2.6 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 46-55, 1989.
Dixon, R. "String Drawings." Ch. 2 in Mathographics. New York: Dover, pp. 75-78, 1991.
Gray, A. "Involutes." §5.4 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 103-107, 1997.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 40-42 and 202, 1972.
Lockwood, E. H. "Evolutes and Involutes." Ch. 21 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 166-171, 1967.
Pappas, T. "The Involute." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 187, 1989.
Yates, R. C. "Involutes." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 135-137, 1952
بر گرفته از سایت mathworld.wolfram.com
برگ درختان سبز در نظر هوشیار هر ورقش دفتری است معرفت کردگار