CirclePi

 

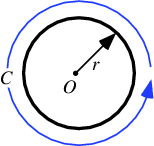
A circle is the set of points in a plane that are equidistant from a given point O. The distance  from the center is called the radius, and the point O is called the center. Twice the radius is known as the diameter d==2r. The angle a circle subtends from its center is a full angle, equal to 360 degrees or 2pi radians.

A circle has the maximum possible area for a given perimeter, and the minimum possible perimeter for a given area.

The perimeter C of a circle is called the circumference, and is given by

C==pid==2pir. (1)

This can be computed using calculus using the formula for arc length in polar coordinates,

C==int_0^(2pi)sqrt(r^2+((dr)/(dtheta))^2)dtheta, (2)

but since r(theta)==r, this becomes simply

C==int_0^(2pi)rdtheta==2pir. (3)

The circumference-to-diameter ratio C/d for a circle is constant as the size of the circle is changed (as it must be since scaling a plane figure by a factor s increases its perimeter by s), and d also scales by s. This ratio is denoted pi (pi), and has been proved transcendental.

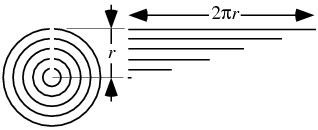
CircleAreaStrips

Knowing C/d, the area of the circle can be computed either geometrically or using calculus. As the number of concentric strips increases to infinity as illustrated above, they form a triangle, so

A==1/2(2pir)r==pir^2. (4)

This derivation was first recorded by Archimedes Eric Weisstein's World of Biography in Measurement of a Circle (ca. 225 BC Eric Weisstein's World of Astronomy).

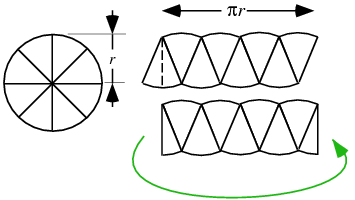
CircleAreaWedges

If the circle is instead cut into wedges, as the number of wedges increases to infinity, a rectangle results, so

A==(pir)r==pir^2. (5)

From calculus, the area follows immediately from the formula

A==int_0^(2pi)dthetaint_0^rrdr==(2pi)(1/2r^2)==pir^2, (6)

again using polar coordinates.

A circle has also be viewed as the limiting case of a regular polygon with inradius r and circumradius R as the number of sides n approaches infinity. This then gives the circumference as

C = lim_(n->infty)2rntan(pi/n)==2pir (7)
= lim_(n->infty)2Rnsin(pi/n)==2piR, (8)

and the area as

A = lim_(n->infty)nr^2tan(pi/n)==pir^2 (9)
= lim_(n->infty)1/2nR^2sin((2pi)/n)==piR^2, (10)

which are equivalently since the radii r and R converge to the same radius as n->infty.

Unfortunately, geometers and topologists adopt incompatible conventions for the meaning of "n-sphere," with geometers referring to the number of coordinates in the underlying space and topologists referring to the dimension of the surface itself (Coxeter 1973, p. 125). As a result, geometers call the circumference of the usual sphere the 2-sphere, while topologists refer to it as the 1-sphere and denote it S^1.

The circle is a conic section obtained by the intersection of a cone with a plane perpendicular to the cone's symmetry axis. It is also a Lissajous curve. A circle is the degenerate case of an ellipse with equal semimajor and semiminor axes (i.e., with eccentricity 0). The interior of a circle is called a disk. The generalization of a circle to three dimensions is called a sphere, and to n dimensions for n>=4 a hypersphere.

The region of intersection of two circles is called a lens. The region of intersection of three symmetrically placed circles (as in a Venn diagram), in the special case of the center of each being located at the intersection of the other two, is called a Reuleaux triangle.

In Cartesian coordinates, the equation of a circle of radius a centered on (x_0,y_0) is

(x-x_0)^2+(y-y_0)^2==a^2. (11)

In pedal coordinates with the pedal point at the center, the equation is

pa==r^2. (12)

The circle having P_1P_2 as a diameter is given by

(x-x_1)(x-x_2)+(y-y_1)(y-y_2)==0. (13)

The parametric equations for a circle of radius a can be given by

x = acost (14)
y = asint. (15)

The circle can also be parameterized by the rational functions

x = (1-t^2)/(1+t^2) (16)
y = (2t)/(1+t^2), (17)

but an elliptic curve cannot.

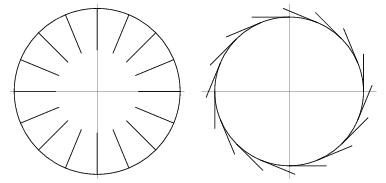
CircleNormalTangent

The plots above show a sequence of normal and tangent vectors for the circle.

The arc length s, curvature kappa, and tangential angle phi of the circle with radius a represented parametrically by (◇) and (◇) are

s(t) = at (18)
kappa(t) = 1/a (19)
phi(t) = t/a. (20)

The Cesàro equation is

kappa==1/a. (21)

In polar coordinates, the equation of the circle has a particularly simple form.

r==a (22)

is a circle of radius a centered at origin,

r==2acostheta (23)

is circle of radius a centered at (a,0), and

r==2asintheta (24)

is a circle of radius a centered on (0,a).

The equation of a circle passing through the three points (x_i,y_i) for i==1, 2, 3 (the circumcircle of the triangle determined by the points) is

|x^2+y^2 x y 1; x_1^2+y_1^2 x_1 y_1 1; x_2^2+y_2^2 x_2 y_2 1; x_3^2+y_3^2 x_3 y_3 1|==0. (25)

The center and radius of this circle can be identified by assigning coefficients of a quadratic curve

ax^2+cy^2+dx+ey+f==0, (26)

where a==c and b==0 (since there is no xy cross term). completing the square gives

a(x+d/(2a))^2+a(y+e/(2a))^2+f-(d^2+e^2)/(4a)==0. (27)

The center can then be identified as

x_0 = -d/(2a) (28)
y_0 = -e/(2a) (29)

and the radius as

r==sqrt((d^2+e^2)/(4a^2)-f/a), (30)

where

a = |x_1 y_1 1; x_2 y_2 1; x_3 y_3 1| (31)
d = -|x_1^2+y_1^2 y_1 1; x_2^2+y_2^2 y_2 1; x_3^2+y_3^2 y_3 1| (32)
e = |x_1^2+y_1^2 x_1 1; x_2^2+y_2^2 x_2 1; x_3^2+y_3^2 x_3 1| (33)
f = -|x_1^2+y_1^2 x_1 y_1; x_2^2+y_2^2 x_2 y_2; x_3^2+y_3^2 x_3 y_3|. (34)

Four or more points which lie on a circle are said to be concyclic. Three points are trivially concyclic since three noncollinear points determine a circle.

In trilinear coordinates, every circle has an equation of the form

(lalpha+mbeta+ngamma)(aalpha+bbeta+cgamma)+k(abetagamma+bgammaalpha+calphabeta)==0 (35)

with k!=0 (Kimberling 1998, p. 219).

The center alpha_0:beta_0:gamma_0 of a circle given by equation (◇) is given by

alpha_0 = l+kcosA-ncosB-mcosC (36)
beta_0 = m-ncosA+kcosB-lcosC (37)
gamma_0 = n-mcosA-lcosB+kcosC (38)

(Kimberling 1998, p. 222).

In exact trilinear coordinates (alpha,beta,gamma), the equation of the circle passing through three noncollinear points with exact trilinear coordinates (alpha_1,beta_1,gamma_1), (alpha_2,beta_2,gamma_2), and (alpha_3,beta_3,gamma_3) is

|abetagamma+bgammaalpha+calphabeta alpha beta gamma; abeta_1gamma_1+bgamma_1alpha_1+calpha_1beta_1 alpha_1 beta_1 gamma_1; abeta_2gamma_2+bgamma_2alpha_2+calpha_2beta_2 alpha_2 beta_2 gamma_2; abeta_3gamma_3+bgamma_3alpha_3+calpha_3beta_3 alpha_3 beta_3 gamma_3|==0 (39)

(Kimberling 1998, p. 222).

An equation for the trilinear circle of radius R with center alpha_0:beta_0:gamma_0 is given by Kimberling (1998, p. 223).

SEE ALSO: Adams' Circle, Arc, Blaschke's Theorem, Brahmagupta's Formula, Brocard Circle, Casey's Theorem, Central Circle, Cevian Circle, Chord, Circle Inscribing, Circle-Line Intersection, Circle Power, Circumcircle, Circumference, Clifford's Circle Theorem, Closed Disk, Concentric Circles, Cosine Circle, Cotes Circle Property, Diameter, Disk, Droz-Farny Circles, Ellipse, Euler Triangle Formula, Excircles, Excosine Circle, Eyeball Theorem, Feuerbach's Theorem, First Lemoine Circle, Five Circles Theorem, Five Disks Problem, Flower of Life, Ford Circle, Fuhrmann Circle, Gerschgorin Circle Theorem, Hart Circle, Hopf Circle, Incircle, Inversive Distance, Kinney's Set, Lens, Lester Circle, Lissajous Curve, Magic Circles, Malfatti Circles, McCay Circles, Midcircle, Monge's Theorem, Neuberg Circles, Nine-Point Circle, Open Disk, P-Circle, Parry Circle, Pi, Point Circle, Polar Circle, Prime Circle, Pseudocircle, Ptolemy's Theorem, Purser's Theorem, Radical Axis, Radius, Reuleaux Triangle, Seed of Life, Seifert Circle, Semicircle, Seven Circles Theorem, Similitude Circle, Six Circles Theorem, Soddy Circles, Sphere, Taylor Circle, Triplicate-Ratio Circle, Tucker Circles, Unit Circle, Venn Diagram, Villarceau Circles, Yin-Yang. [Pages Linking Here]

REFERENCES:

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 125 and 197, 1987.

Casey, J. "The Circle." Ch. 3 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 96-150, 1893.

Coolidge, J. L. A Treatise on the Geometry of the Circle and Sphere. New York: Chelsea, 1971.

Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 74-75, 1996.

Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973.

Coxeter, H. S. M. and Greitzer, S. L. "Some Properties of the Circle." Ch. 2 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 27-50, 1967.

Dunham, W. "Archimedes' Determination of Circular Area." Ch. 4 in Journey through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 84-112, 1990.

Eppstein, D. "Circles and Spheres." http://www.ics.uci.edu/~eppstein/junkyard/sphere.html.

Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 1, 1999.

Kern, W. F. and Bland, J. R. Solid Mensuration with Proofs, 2nd ed. New York: Wiley, p. 3, 1948.

Kimberling, C. "Triangle Centers and Central Triangles." Congr. Numer. 129, 1-295, 1998.

Lachlan, R. "The Circle." Ch. 10 in An Elementary Treatise on Modern Pure Geometry. London: Macmillian, pp. 148-173, 1893.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 65-66, 1972.

MacTutor History of Mathematics Archive. "Circle." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Circle.html.

Pappas, T. "Infinity & the Circle" and "Japanese Calculus." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 68 and 139, 1989.

Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., 1995.

Yates, R. C. "The Circle." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 21-25, 1952

برگرفته از سایت mathworld.wolfram.com